Rumus Kesebangunan
Rumus Kesebangunan (Tugas)
Rumus Kesebangunan
Dua bangun dikatakan sebangun jika
a. panjang sisi-sisi yang bersesuaian dari kedua bangun tersebut memiliki perbandingan senilai
b. sudut-sudut yang bersesuaian dari kedua bangun tersebut sama besar.
2. Bangun-bangun yang memiliki bentuk dan ukuran yang sama dikatakan bangun-bangun yang kongruen.
3. Syarat dua segitiga sebangun adalah sisi-sisi yang bersesuaian sebanding atau sudut-sudut yang bersesuaian sama besar.
4. Syarat dua segitiga kongruen:
a. Sisi-sisi yang bersesuaian sama panjang (s.s.s)
b. Dua sisi yang bersesuaian sama panjang dan sudut yang diapitnya sama besar (s.sd.s)
c. Dua sudut yang bersesuaian sama besar dan sisi yang berada di antaranya sama panjang (sd.s.sd)
d. Dua sudut yang bersesuaian sama besar dan sisi yang berada di hadapannya sama panjang (sd.sd.s).
Yang pertama : untuk kasus siku-siku

Yang kedua : untuk segitiga sembarang

Penurunan rumus kesebangunan
Berapa panjang PQ jika AB (sisi yang panjang) dan DC (sisi yang pendek) diketahui panjangnya dan perbandingan AP : AC = BQ : BD diketahui.
Jawabannya ADA, simaklah ulasan berikut ini! Langsung aja ke TKP. hehehe
Pada posting sebelumnya, House of Math sudah mengulas cara menyelesaikan soal tersebut. Namun cara yang digunakan lumayan panjang. Nah sekarang House of Math akan mengulas tentang rumus cepat untuk menyelesaikan soal tersebut.
Dengan menggunakan proses berfikir pada posting pembahasan soal tersebut, kita bisa menurunkan rumus cepatnya. Inilah caranya:
1. Kita buat perpanjangan garis PQ di R
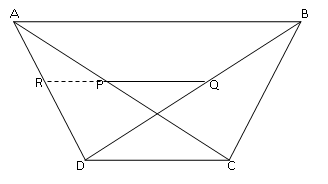
2. Misal = AP : AC = BQ : BD = m : n
3. Selanjutnya Pandang segitiga ADC
Berlaku hubungan:
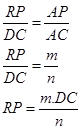
4. Pandang segitiga ABD

Berlaku hubungan:
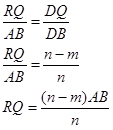
5. RQ merupakan sebuah garis yang dapat dibentuk olah garis RP dan garis RQ sehingga:
6. Sehingga untuk menghitung panjang PQ dapat langsung menggunakan rumus :
Dengan:
AB = sisi yang panjang
DC = sisi yang pendek
m : n = perbandingan letak P dan Q (kecil : besar)
Sekian penurunan rumus cepatnya, sepanjang itu menghasilkan rumus yang singkat,yang cepat, yang memudahkan pengerjaan soal.

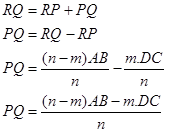
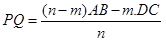



0 komentar:
Posting Komentar